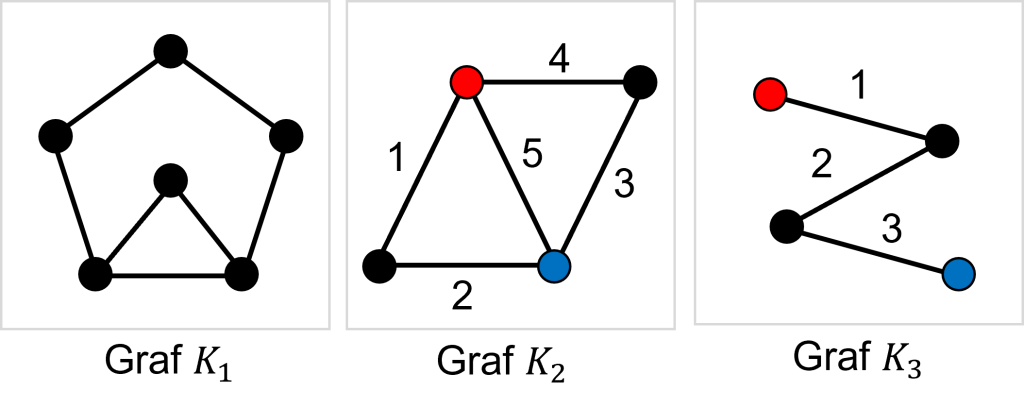
 Ilustrasi Graf (Foto:mathcyber1997.com)
Ilustrasi Graf (Foto:mathcyber1997.com)
Graf adalah salah satu konsep fundamental dalam matematika dan ilmu komputer yang merepresentasikan hubungan antar objek. Struktur graf terdiri dari simpul (vertex) dan sisi (edge) yang menghubungkan simpul-simpul tersebut. Dengan kemampuannya untuk memodelkan berbagai jenis hubungan dan interaksi, graf telah menjadi alat yang sangat berguna dalam banyak disiplin ilmu, mulai dari matematika dan ilmu komputer hingga biologi dan ilmu sosial.
Konsep graf sudah ada sejak abad ke-18, ketika matematikawan Swiss, Leonhard Euler, menyelesaikan masalah jembatan Königsberg. Masalah ini melibatkan mencari rute yang memungkinkan seseorang untuk berjalan melalui semua jembatan di kota Königsberg tanpa mengulang rute. Dari penelitian ini, Euler menciptakan dasar bagi teori graf, yang kini menjadi cabang penting dalam matematika (Diestel, 2017).
Graf dapat diklasifikasikan menjadi beberapa jenis berdasarkan sifat dan struktur mereka. Salah satu jenis graf adalah graf tak berarah (undirected graph), di mana sisi tidak memiliki arah, sehingga hubungan antara simpul bersifat dua arah. Contohnya adalah jaringan sosial, di mana hubungan antar individu dapat terjadi dalam kedua arah. Di sisi lain, graf berarah (directed graph) memiliki sisi yang menunjukkan arah, menggambarkan hubungan satu arah antara simpul, seperti dalam representasi situs web dan hyperlink (Cormen et al., 2009).
Aplikasi graf sangat luas dan mencakup berbagai bidang. Dalam ilmu komputer, graf digunakan untuk memecahkan masalah seperti pencarian jalur terpendek, penjadwalan, dan pemrosesan jaringan. Algoritma Dijkstra dan A* adalah contoh algoritma yang digunakan untuk menemukan jalur terpendek dalam graf. Selain itu, dalam analisis jaringan sosial, graf digunakan untuk merepresentasikan hubungan antar individu atau kelompok, membantu memahami dinamika sosial dan pola interaksi (West, 2001).
Di bidang biologi, graf digunakan untuk memodelkan jaringan interaksi antar spesies, seperti jaringan makanan, dan dalam pemetaan genetik untuk menunjukkan hubungan antara gen. Dalam ekonomi, graf dapat digunakan untuk memodelkan interaksi pasar, hubungan antara produsen dan konsumen, serta aliran barang dan jasa (Bollobás, 1998).
Keindahan matematika dalam graf terletak pada cara mereka menyajikan kompleksitas dan keterhubungan dalam struktur yang sederhana. Graf dapat digunakan untuk menganalisis dan memvisualisasikan data dengan cara yang intuitif, memberikan wawasan baru yang mungkin tidak terlihat dengan metode analisis lain. Dengan berkembangnya teknologi dan komputasi, penggunaan graf semakin luas, terutama dalam analisis big data dan pembelajaran mesin. Graf memberikan kerangka kerja yang kuat untuk memahami hubungan dan pola dalam data yang kompleks (Koshy, 2001).
Graf adalah alat yang sangat penting dan menarik dalam matematika dan berbagai bidang ilmu lainnya. Dari memahami struktur sosial hingga memecahkan masalah algoritmik, graf menawarkan cara yang unik untuk merepresentasikan dan menganalisis hubungan. Dengan kemampuannya untuk menyederhanakan kompleksitas dan menyajikan informasi dengan cara yang jelas, graf adalah contoh nyata dari keindahan dan kekuatan matematika.
Kata Kunci: Graf, Teori Graf, Jaringan, Aplikasi Matematika, Algoritma, Struktur Data
Referensi
Diestel, R. (2017). Graph Theory. Springer.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms. MIT Press.
West, D. B. (2001). Introduction to Graph Theory. Prentice Hall.
Bollobás, B. (1998). Modern Graph Theory. Springer.
Koshy, T. (2001). Fibonacci and Lucas Numbers with Applications. Wiley-Interscience. http://doi.org/10.1002/9781118033067.
 Penulis: Silvina Rosita Yulianti
Penulis: Silvina Rosita Yulianti
