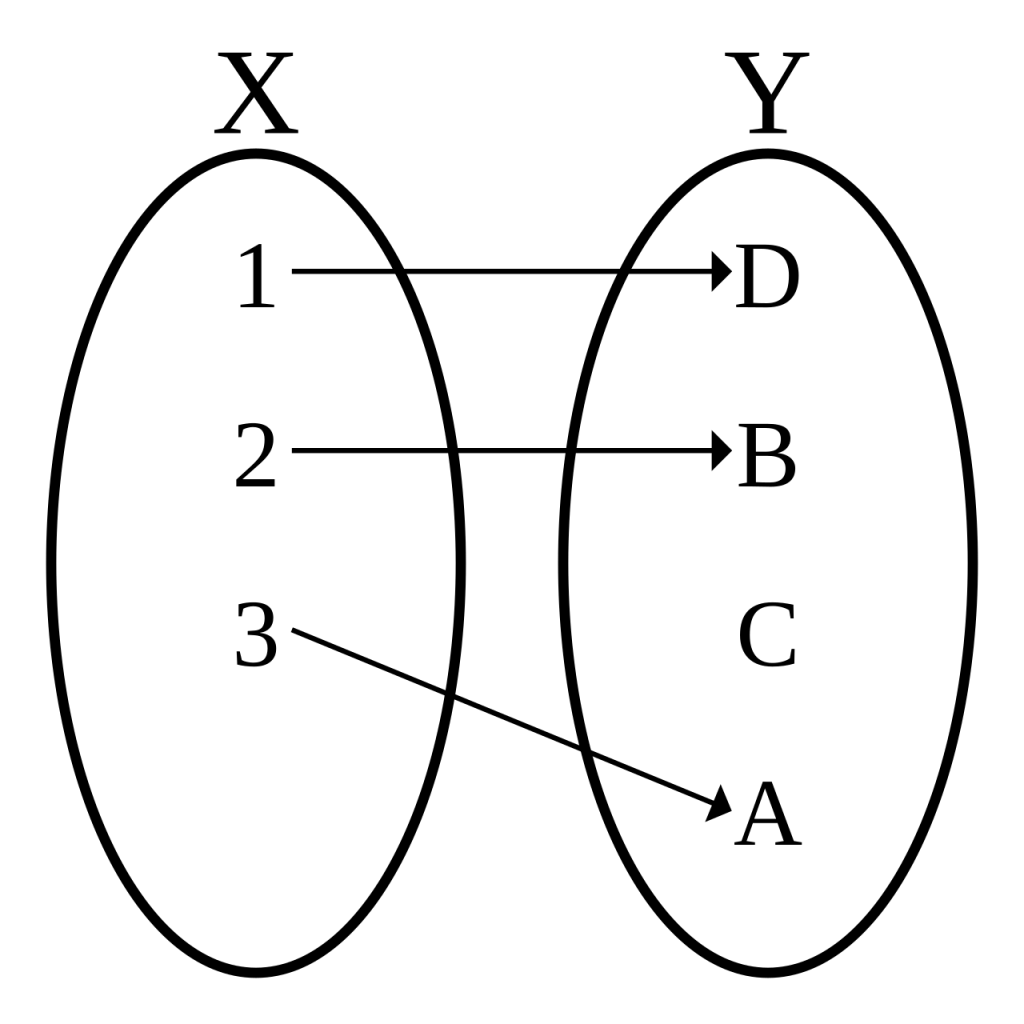
Mengenal Fungsi Injektif: Apa Itu dan Mengapa Penting?

Dalam matematika, fungsi adalah aturan yang menghubungkan setiap elemen dari satu himpunan (disebut domain) ke elemen dalam himpunan lain (disebut kodomain). Salah satu jenis fungsi yang sering muncul di berbagai bidang adalah fungsi injektif, yang sering disebut sebagai fungsi satu-ke-satu. Fungsi ini memiliki sifat khusus yang membedakannya dari jenis fungsi lainnya. Dalam artikel ini, kita akan membahasnya dengan sederhana dan menyeluruh.

Definisi Fungsi Injektif

Fungsi $f:A\toB$ dikatakan injektif (atau satu-ke-satu) jika setiap elemen berbeda di himpunan $A$ dipetakan ke elemen berbeda di himpunan $B$ . Secara formal, jika $x$ dan $y$ ada di $A$ dan $f(x)=f(y)$ , maka $x=y$ . Artinya, tidak ada dua elemen berbeda di $A$ yang memiliki hasil yang sama di $B.$

Definisi Alternatif Fungsi Injektif

Selain definisi formal sederhana di atas, terdapat beberapa definisi ekuivalen lainnya yang dapat membantu kita memahami fungsi injektif dengan lebih baik:

Definisi Kontrapositif: Fungsi $f:A\toB$ bersifat injektif jika untuk setiap $x$ dan $y$ di $A$ , jika $x\neqy$ , maka $f(x)\neqf(y)$ .
Definisi Berdasarkan Subhimpunan: Fungsi $f:A\toB$ bersifat injektif jika untuk setiap subhimpunan $X$ dan $Y$ di $A$ , jika $X\subseteqY$ , maka $f(Y∖X)=f(Y)∖f(X)$ . Ini berarti fungsi injektif mempertahankan struktur subhimpunan.
Definisi Berdasarkan Irisan Himpunan: Fungsi $f:A\toB$ bersifat injektif jika untuk setiap subhimpunan $X$ dan $YY$ di $A$ , jika $X\capY=\emptyset$ , maka $f(X)\capf(Y)=\emptyset$ . Dengan kata lain, fungsi ini memastikan bahwa citra dari dua himpunan yang saling lepas tidak saling beririsan.
Definisi Berdasarkan Preimage dan Image: Fungsi $f:A\toB$ bersifat injektif jika untuk setiap subhimpunan $X$ di $A$ , preimage dari citra $X$ sama dengan $X$ itu sendiri. Preimage dari suatu himpunan adalah semua elemen di domain yang dipetakan ke elemen di $Y$ , sedangkan citra dari suatu himpunan $X$ adalah himpunan semua $f(x)f(x)$ dengan $x$ di $X$ . Ini menunjukkan bahwa fungsi injektif memetakan setiap elemen di $A$ ke elemen unik di $B$ .

Mengapa Fungsi Injektif Penting?

Fungsi injektif muncul dalam berbagai konteks dan aplikasi matematika. Fungsi ini sangat berguna dalam teori himpunan, aljabar, analisis, dan bidang lainnya. Salah satu aplikasinya adalah untuk memahami kesamaan struktur antara dua objek matematika seperti grup, gelanggang, modul, ruang vektor, dan sebagainya. Dalam kriptografi, fungsi injektif digunakan untuk mengenkripsi informasi dengan memastikan setiap pesan dikodekan menjadi nilai yang berbeda. Fungsi injektif juga sangat penting dalam teori kategori, yang mempelajari hubungan antara objek matematika secara lebih abstrak.

Kesimpulan

Fungsi injektif adalah konsep fundamental dalam matematika yang penting untuk memahami bagaimana objek dapat dipetakan dari satu himpunan ke himpunan lainnya. Dengan sifatnya yang unik, fungsi injektif memastikan bahwa tidak ada dua elemen berbeda yang dipetakan ke elemen yang sama. Berbagai definisi ekuivalen menawarkan pemahaman yang lebih luas tentang karakteristik fungsi ini, memungkinkan penerapan konsep injektif dalam berbagai aplikasi matematika dan sains.

Kata Kunci: Fungsi, Injektif, Matematika

Referensi:

Surodjo, B., Wahyuni, S., Sutopo, Wijayanti, I.E., Susanti, Y., Sutjijana, A., Ferrari, O., 2024, Logika Matematika dan Himpunan, Deepublish.

Soehakso, Diktat Pengantar Matematika Modern, Departemen Matematika FMIPA UGM.

Penulis: Yeni Susanti