Graf Cayley adalah salah satu konsep penting dalam matematika, terutama dalam bidang teori grup dan graf. Meski terdengar teknis, ide dasarnya sederhana dan sangat menarik. Graf ini menawarkan cara visual untuk merepresentasikan struktur aljabar grup, yang menjadikannya alat penting dalam berbagai bidang seperti matematika murni, ilmu komputer, dan fisika. Graf Cayley pertama kali diperkenalkan oleh Arthur Cayley pada abad ke-18, yang kemudian diperkenalkan ulang oleh Max Dehn sebagai diagram grup (gruppenbild) pada lecture note yang tidak dipublikasikan.
Apa itu Graf Cayley?
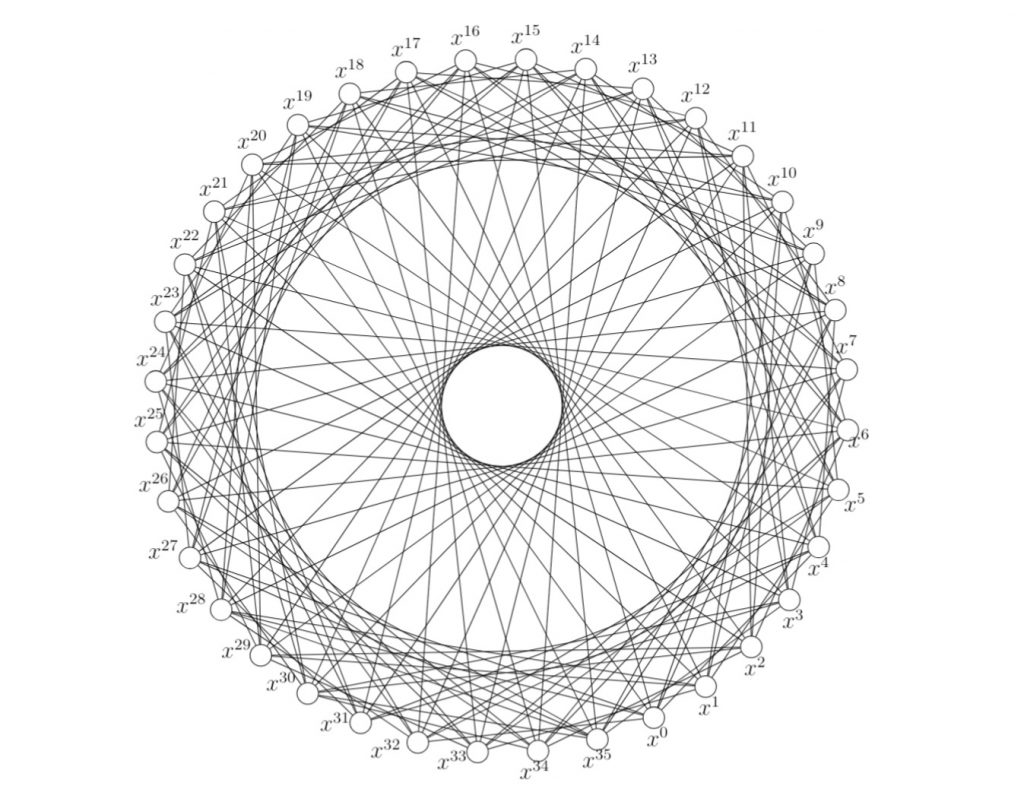
Graf Cayley adalah graf yang dikonstruksi dari grup G dan himpunan penghubung S yang merupakan himpunan bagian dari G yang tidak memuat elemen identitas grup, serta tertutup terhadap invers elemen. Dalam graf Cayley ini,
- setiap titiknya merepresentasikan elemen dari grup G, dan
- setiap sisinya menghubungkan dua titik jika salah satu titik tersebut dapat diperoleh dari titik yang lain dengan mengalikan salah satu elemen di S.
Keindahan Graf Cayley
Graf Cayley tidak hanya menarik secara visual tetapi juga menyimpan banyak informasi tentang grup yang direpresentasikannya. Beberapa karakteristik dasar graf Cayley diantaranya adalah:
- Derajat setiap titiknya selalu sama dengan banyaknya elemen S.
- Graf Cayley atas grup G dengan himpunan penghubung S merupakan graf yang terhubung jika dan hanya jika G dibangun oleh S.
- Graf Cayley merupakan graf yang bersifat transitif titik (vertex transitive), yang mana untuk setiap pasang dua titiknya, selalu dapat ditemukan isomorfisma graf yang membawa satu titik diantaranya ke titik yang lain.
Selain itu, graf Cayley juga berperan di ranah aplikasi multidisiplin: Dalam fisika, misalnya, graf Cayley digunakan dalam teori jaringan dan kristalografi untuk mempelajari simetri molekul. Selain itu, dalam aplikasi modern graf Cayley juga berperan pada bidang-bidang sebagai berikut:
- Ilmu Komputer: Graf Cayley sering digunakan dalam teori jaringan untuk mendesain arsitektur jaringan komputer yang efisien, seperti jaringan hypercube dan torus.
- Fisika: Dalam studi sistem kristal dan dinamika molekul, graf ini membantu memahami simetri dan hubungan antarpartikel.
- Kriptografi: Struktur aljabar grup dalam graf Cayley sering dimanfaatkan untuk mengembangkan algoritma kriptografi berbasis grup.
Graf Cayley adalah contoh luar biasa bagaimana matematika abstrak dapat divisualisasikan dengan cara yang intuitif dan menarik. Konsep ini menghubungkan teori grup dengan graf, menciptakan jembatan yang memungkinkan aplikasi di berbagai disiplin ilmu. Dengan mempelajari graf Cayley, kita tidak hanya menggali lebih dalam keindahan matematika, tetapi juga membuka pintu ke berbagai penerapan di dunia nyata.
Kata Kunci: Graf, Cayley, Aljabar.
Referensi:
- Godsil, C., & Royle, G. (2001), Algebraic Graph Theory, Springer.
- Biggs, N. L. (1993), Algebraic Graph Theory, Cambridge University Press.
- Diestel, R. (2017), Graph Theory, Springer.
- Babai, L. (1995), Graph Isomorphism in Quasipolynomial Time. Proceedings of the 48th-Annual ACM Symposium on Theory of Computing.
- Susanti, Y., Erfanian, A., (2024), 2024, Prime Square Order Cayley Graph of Cyclic Groups, Asian European Journal of Mathematics (AEJM), Vol 17 (2) 2450003 2024 https://doi.org/10.1142/S1793557124500037
 Penulis: Yeni Susanti
Penulis: Yeni Susanti
