A Characterization of Cut Set on Semilattice-Valued Fuzzy Sets

The research entitled “A Characterization of Cut Set on Semilattice-Valued Fuzzy Sets” was conducted by Harina Orpa Lefina Monim under the guidance of Prof. Dr. Sri Wahyuni, MS. and Dr. Indah Emilia W., M.Si. in 2018.

The following is the abstract of this research.

ABSTRACT

Semilattice $(S,\leq)$ is a partially ordered set which a pair of its elements have infimum or supremum. When it is equipped by an equivalence relation defines as $p\approx_{M} q \iff \uparrow p \cap M = \uparrow q \cap M$ for any $p, q \in S$ where $M\subseteq S, M\neq \emptyset$ and $\uparrow p$ and $\uparrow q$ are principle filters generated by $p,q$ respectively. Semilattice $S$ is partitioned into equivalence classes- $\approx M$ . A collection of the classes- $\approx M$ forms a poset under inclusion. We call the collection as a quotient set and denoted $S/ \approx M$ . The quotient set is a poset under inclusion. Generally, the poset of a quotient set is not a semilattice.

On a semilattice valued fuzzy set $\mu: X\rightarrow S$ , we replace $S$ by the semilattice $S$ equipped by relation $\approx_{M}$ on $S$ above. For any $p\in S$ , a cut set will be defined by $\mu_{p}=\{x\in X \mid p\leq \mu(x)\}$ . Then a collection of all of cut sets, denoted $\mu_{S}$ , is a poset by inclusion. Inverse function of $\mu$ from $\uparrow p \cap M$ , denoted $\mu^{-1}(\uparrow p\cap M)$ , will determine a characteristic function for any $p\in S$ . The characteristic function of $\mu^{-1}(\uparrow p\cap M)$ along with $p\in S$ is

$\begin{equation*} M_{p} : X\rightarrow {0,p}, \end{equation*}$

by definition:

(1) $\begin{equation*} M_{p}(x)=\begin{cases} p, & x\in \mu^{-1}(\uparrow p\cap M)\vspace*{0.2cm}\\ 0, & \text{others.} \end{cases} \end{equation*}$

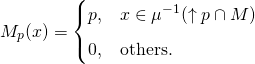
Furthermore, the collection of characteristic function indexed by $p\in S$ , $\mathcal{M}_{S}=\{M_{p}\mid p\in S\}$ , is a collection of all subsets of $X\neq 0$ . We use this collection for a sinthesys theorem on the semillatice valued fuzzy set. We will investigate a sufficient and necessary condition for $\mathcal{M}_{S}$ to be the collection of all cuts sets of $\mu \in S^{X}$ . On the other hand we will present a concept of semi closure system and its dual. Then we will present also the isomorphism between the two collections. Using this property we investigate sufficient and necessary conditions for two semilattices pvalued fuzzy sets to have a coincide collection of cuts sets.

The main result is a collection of cut sets of semilattice valued fuzzy sets is the family $\mathcal{M}_{S}=\{M_{p}\mid p\in S\}$ . This family of cut sets is a semi closure system on $X$ when $S$ is a complete join semilattice. However, the family of cut sets is dual semi closure system on $X$ when $S$ is complete meet semilattice. Another result is any two of semilattice valued fuzzy sets $\mu, v\in S^{X}$ have a coincide collection of cut sets.

Keywords: Semilattices, fuzzy sets, cuts, semi closure systems, and dual semi closure systems.