Karakteristik Himpunan Potongan Dari Himpunan Fuzzy Bernilai Semilatis

Penelitian dengan judul “Karakteristik Himpunan Potongan Dari Himpunan Fuzzy Bernilai Semilatis” dilakukan oleh Harina Orpa Lefina Monim dibawah bimbingan Prof. Dr. Sri Wahyuni, MS. dan Dr. Indah Emilia W., M.Si. pada tahun 2018.

Berikut ini merupakan intisari dari penelitian tersebut.

INTISARI

Semilatis $(S,\leq)$ merupakan himpunan terurut parsial yang setiap pasang elemen mempunyai infimum atau supremum. Semilatis yang dilengkapi relasi ekuivalensi dengan definisi $p\sim_{M} q \iff \uparrow p \cap M=\uparrow q\cap M$ untuk setiap $p,q\in S$ dengan $M\subseteq S$ , $M\neq \emptyset$ dan $\uparrow p, \uparrow q$ berturut-turut filter yang dibangkitkan oleh $p,q$ menyebabkan terbentuknya kelas-kelas ekuivalensi. Koleksi kelas-kelas ekuivalensi disebut himpunan kuosien dan dinotasikan $S/\sim_{M}$ . Himpunan kuosien $S/\sim_{M}$ merupakan poset terhadap relasi urutan inklusi. Himpunan kuosien umumnya tidak membentuk semilatis.

Pada $\mu : X \rightarrow S$ himpunan fuzzy bernilai semilatis pada $X$ diambil $S$ semilatis yang dilengkapi dengan relasi ekivalensi $\sim_{M}$ seperti di atas. Untuk $p\in S$ , himpunan bagian dari domain X disebut himpunan potongan $\mu_{p}=\{x\in X\mid p\leq \mu(x)\}$ . Koleksi semua himpunan potongan yang dinotasikan dengan $\mu_{S}$ , membentuk poset terhadap relasi inklusi. Invers fungsi $\mu$ dari $\uparrow p \cap M$ , dinotasikan $\mu^{-1}(\uparrow p\cap M)$ , menentukan fungsi karakteristik untuk setiap $p\in S$ . Fungsi karakteristik dari $\mu^{-1}(\uparrow p\cap M)$ dengan $p\in S$ adalah $M_{p}: X\rightarrow \{0,p\}$ yang di definisikan:

$\begin{equation*} M_{p}=\begin{cases} p, & x\in \mu^{-1}(\uparrow p\cap M)\vspace*{0.5cm}\\ 0, & \text{lainnya.} \end{cases} \end{equation*}$

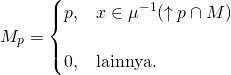
Selanjutnya, koleksi fungsi karakteristik yang diindeks oleh $p\in S$ yaitu $\mathcal{M}_{S}=\{M_{p}\mid p\in S\}$ , merupakan koleksi himpunan bagian dari himpunan tak kosong $X$ . Koleksi $\mathcal{M}_{S}$ digunakan untuk membangun teorema sintesa melalui himpunan fuzzy bernilai semilatis $S$ . Akan dikaji syarat cukup koleksi $\mathcal{M}_{S}=\{M_{p}\mid p\in S\}$ merupakan koleksi semua himpunan potongan dari $\mu \in S^{X}$ . Pada sisi lain disajikan konsep sistem semi klosur dan sistem dualnya. Selanjutnya, diselidiki kapan koleksi semua potongan merupakan sistem semi klosur dan sistem dual semi klosur. Lebih lanjut lagi disajikan hubungan isomorfisma antara koleksi himpunan potongan dan koleksi bayangan. Berdasarkan sifat tersebut dikaji syarat perlu dan cukup koleksi potongan dari dua himpunan fuzzy bernilai semilatis $\mu, v\in S^{X}$ .

Hasil yang diperoleh adalah koleksi potongan dari himpunan fuzzy bernilai semilatis $S$ merupakan keluarga himpunan bagian $\mathcal{M}_{S}=\{M_{p}\mid p\in S\}$ yang bersifat semi klosur yaitu klosur yang diperlemah atas himpunan tak kosong $X$ . Hasil lainnya adalah dua himpunan fuzzy bernilai semilatis mempunyai koleksi potongan yang bersesuaian.

Kata-kata kunci: semilatis, himpunan fuzzy, himpunan potongan, sistem semi klosurdan sistem dual semi klosur.