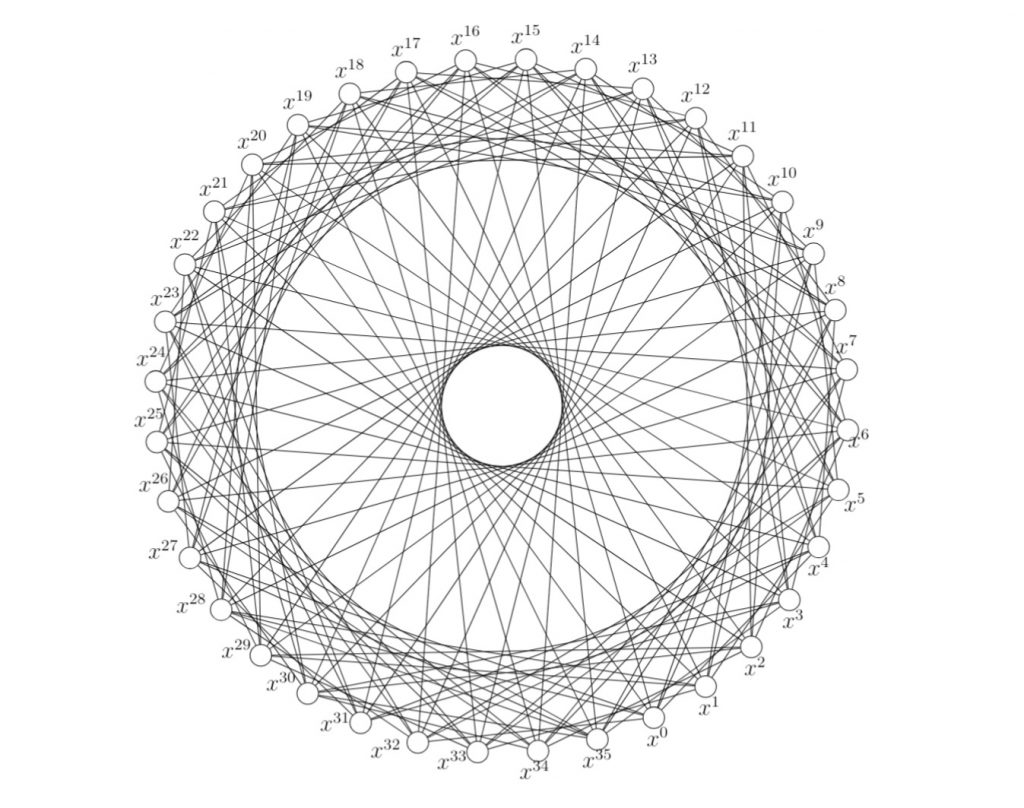
The Cayley graph is an important concept in mathematics, particularly in the field of group theory and graph theory. Although it sounds technical, its basic idea is simple and very interesting. This graph provides a visual way to represent the algebraic structure of a group, making it an important tool in various fields such as pure mathematics, computer science, and physics. The Cayley graph was first introduced by Arthur Cayley in the 18th century, and was later reintroduced by Max Dehn as a group diagram (gruppenbild) in unpublished lecture notes.
What is a Cayley Graph?
A Cayley graph is a graph constructed from a group G and a set of generators S, which is a subset of G that does not contain the identity element of the group and is closed under the inverse of the elements. In this Cayley graph, each vertex represents an element of the group G, and each edge connects two vertices if one vertex can be reached from the other by multiplying it by an element from S.
The Beauty of Cayley Graphs
The Cayley graph is not only visually appealing but also contains a lot of information about the group it represents. Some basic characteristics of Cayley graphs include:
– The degree of each vertex is always equal to the number of elements in S.
– A Cayley graph on a group G with a generating set S is connected if and only if G is generated by S.
– Cayley graphs are vertex-transitive, meaning for every pair of vertices, there is always an isomorphism of the graph that maps one vertex to the other.
Moreover, Cayley graphs also play a role in various multidisciplinary applications:
– In physics, for example, Cayley graphs are used in network theory and crystallography to study molecular symmetry.
– In modern applications, Cayley graphs also play a role in areas such as:
– Computer Science: Cayley graphs are often used in network theory to design efficient computer network architectures, such as hypercube and torus networks.
– Physics: In the study of crystal systems and molecular dynamics, these graphs help to understand symmetries and relationships between particles.
– Cryptography: The algebraic structure of groups in Cayley graphs is often utilized to develop group-based cryptographic algorithms.
Cayley graphs are an outstanding example of how abstract mathematics can be visualized in an intuitive and engaging way. This concept links group theory with graphs, creating a bridge that allows for applications in various scientific disciplines. By studying Cayley graphs, we not only explore the beauty of mathematics but also open the door to many real-world applications.
Keywords: Graph, Cayley, Algebra.
References:
– Godsil, C., & Royle, G. (2001), Algebraic Graph Theory, Springer.
– Biggs, N. L. (1993), Algebraic Graph Theory, Cambridge University Press.
– Diestel, R. (2017), Graph Theory, Springer.
– Babai, L. (1995), Graph Isomorphism in Quasipolynomial Time. Proceedings of the 48th-Annual ACM Symposium on Theory of Computing.
– Susanti, Y., Erfanian, A. (2024), Prime Square Order Cayley Graph of Cyclic Groups, Asian European Journal of Mathematics (AEJM), Vol 17 (2) 2450003 2024 https://doi.org/10.1142/S1793557124500037
 Author: Yeni Susanti
Author: Yeni Susanti
