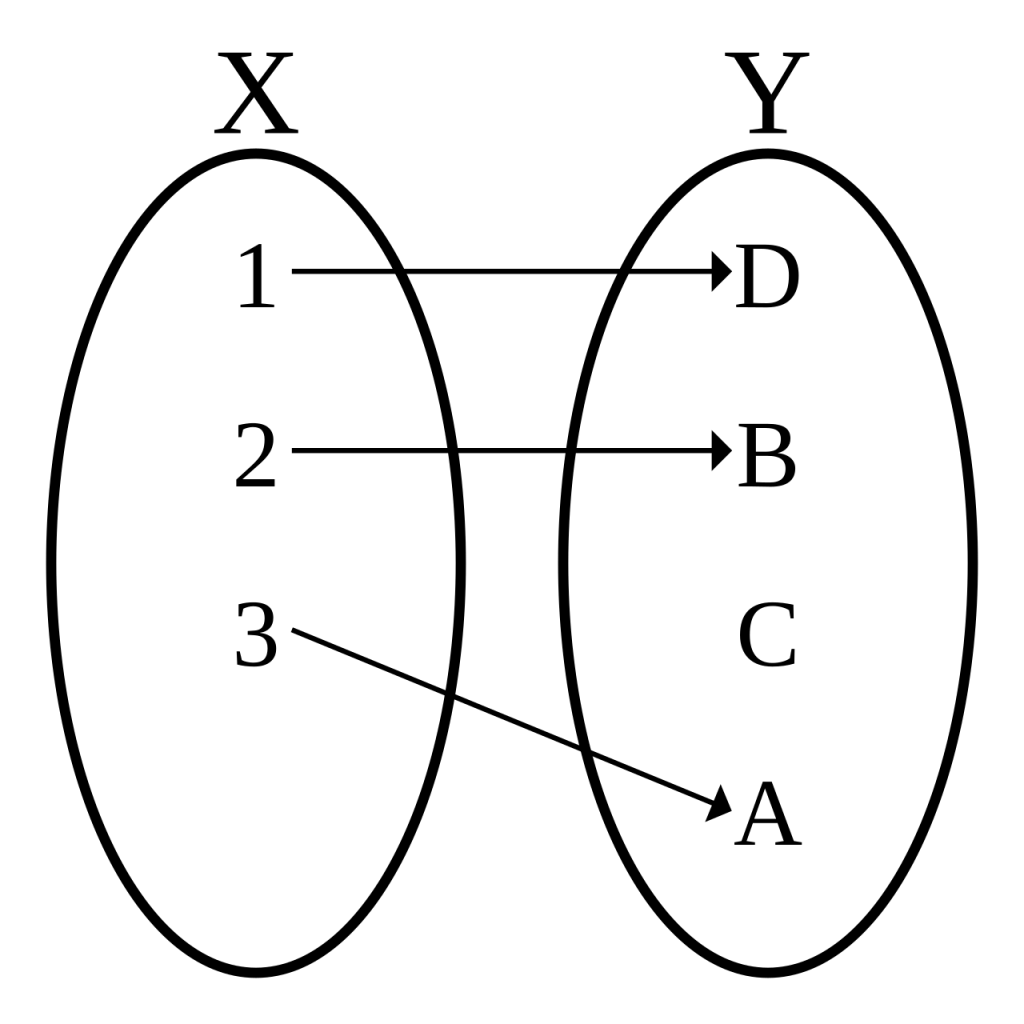
In mathematics, a function is a rule that connects each element of one set (called the domain) to an element in another set (called the codomain). One type of function that frequently appears in various fields is the injective function, often referred to as a one-to-one function. This function has special properties that distinguish it from other types of functions. In this article, we will discuss it simply and comprehensively.
Definition of Injective Function
A function f: A → B is said to be injective (or one-to-one) if every distinct element in set A is mapped to a distinct element in set B. Formally, if x and y are in A and f(x) = f(y), then x = y. This means that no two distinct elements in A can have the same image in B.
Alternative Definitions of Injective Function
In addition to the simple formal definition above, there are several other equivalent definitions that can help us better understand injective functions:
-
Contrapositive Definition: A function f: A → B is injective if for every x and y in A, if x ≠ y, then f(x) ≠ f(y).
-
Definition Based on Subsets: A function f: A → B is injective if for every subset X and Y in A, if X is contained in Y, then f(Y \ X) = f(Y) \ f(X). This means that injective functions preserve the structure of subsets.
-
Definition Based on Set Intersections: A function f: A → B is injective if for every subset X and Y in A, if the intersection of X and Y is empty, then the intersection of f(X) and f(Y) is also empty. In other words, this function ensures that the images of two disjoint sets do not intersect.
-
Definition Based on Preimage and Image: A function f: A → B is injective if for every subset X in A, the preimage of the image of X is equal to X itself. The preimage of a set Y refers to all the elements in the domain that map to elements in Y, and the image of a set X is the set of all f(x) with x in X. This indicates that an injective function maps each element in A to a unique element in B.
Why Are Injective Functions Important?
Injective functions appear in various mathematical contexts and applications. They are highly useful in set theory, algebra, analysis, and other fields. One of their applications is in understanding the structural similarity between two mathematical objects such as groups, rings, modules, vector spaces, and more. In cryptography, injective functions are used to encrypt information by ensuring that each message is encoded into a distinct value. Injective functions are also crucial in category theory, which studies the relationships between mathematical objects in a more abstract way.
Conclusion
Injective functions are a fundamental concept in mathematics that are crucial for understanding how objects can be mapped from one set to another. With their unique properties, injective functions ensure that no two distinct elements are mapped to the same element. Various equivalent definitions offer a broader understanding of the characteristics of this function, allowing us to apply the concept of injectivity in various mathematical and scientific applications.
Keywords: Function, Injective, Mathematics
References:
Surodjo, B., Wahyuni, S., Sutopo, Wijayanti, I.E., Susanti, Y., Sutjijana, A., Ferrari, O., 2024, Logika Matematika dan Himpunan, Deepublish.
Soehakso, Diktat Pengantar Matematika Modern, Departemen Matematika FMIPA UGM.
Author: Yeni Susanti